How to measure by Vernier Calipers
Many of you science students may have seen Vernier Caliper.... somthing like this...
Fig.1
The thing that we are now concerned wiyh is the two scales, so the picture stands as following...
The thing that we are now concerned wiyh is the two scales, so the picture stands as following...
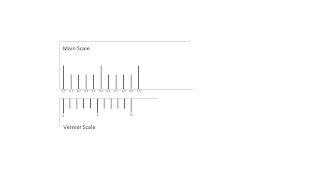
Fig.2
If you are having problem download the picture and magnify it to have a clear view.
You can clearly see that it consists of two parallel scales-
1. Main Scale:- This is the upper scale in the image. This scale is similar to a ruler. Again each unit in this scale is divide into ten decimal points, that is, ten subdivisions to measure the 1/10 th points in a unit.
2. Vernier Scale or Secondary Scale:- This is obviously the most important scale as the name suggests and this is where the cleverness of Mr. Vernier lies. As the image suggests, this scale has ten divisions which is equal to 9 subdivisions of each unit in the main scale.
From the above discussions, it is clearly evident that the exact spacing between each mark in the vernier scale is exactly 0.09 units of the main scale. (As for 10 units in vernier scale, there are 0.9 units in the main one....
therefore for 1 unit in a main scale, there will be 0.9/10= 0.09 units.)
Therefore it is evident that when the 0 of vernier scale is displaced from the 0 of the main scale, then atleast one mark will be closest or perfectly match with a mark on the main scale.
Take the following image as an example:
Fig.3
Here the zero is moved to somewhere between 0.3 and 0.4 in the main scale, so the measurement is 0.3something.
Now just think about it... in its initial position, zero of vernier and zero of main was exactly matching, but the '1' in the vernier was moved away 0.09 units away from 0.0. From the Fig.2, it can be seen that the nearest mark in the main scale of the vernier mark '1' is '0.1'. Since the spacing between each mark in the vernier scale is 0.09 and of main scale is 0.1, so vernier '1' is away from main '0.1' by 0.01 units (0.1-0.09). Similarly the 2 of vernier is 0.08 units away from 0.2 of main scale and so on.
You can notice that after 10 such repeatations, vernier's 10 will obviously match with 0.9 of main. This is because between each mark in the main scale, if we divide them in 10 equal divisions, then according to the figure, the space between the '0.n' th reading in the main scale and the 'n'th reading in the vernier scale will be 0.0n (where 'n' is any whole number). For example, the distance between 0.8 in the main scale and 8 in vernier scale will be 0.08.
Therefore, the space is decreasing by 0.01,
so after 10 such repeatations, the vernier mark will get back from main scale by (0.01x10=) 0.1.
Thus, at 10 it will match with (1.0-0.1=) 0.9.
Now, when the vernier scale is moved, atleast one vernier mark will match with a mark in the main scale, this is because every mark in vernier is backed from its corresponding main scale mark by 0.01 times of that vernier mark, and this continues for every number from 0 to 9. This is a bit difficult to understand. This simply means that the space between the vernier mark and its corresponding mark are 0 and all the first 9 multiples of 0.01, . So, when the vernier scale is moved, atleast one mark in vernier will cross atleast 0.01 units.



No comments:
Post a Comment